弦 (音律) の実験
これでピタゴラス音律の1:2:3の音が楽しめる
同じものを作って同時に鳴らすと面白い
同じものを作って同時に鳴らすと面白い
ますは基本波

2倍(1オクターブ上)波

3倍波 (右を鳴らす)


2倍(1オクターブ上)波

3倍波 (右を鳴らす)

弦の振動は音響物理だけでなく,電磁気学や半導体理論に量子論(超弦理論
も!)などにも登場する.
このような簡単な装置を作って遊んでみると理解が深まるだろう.
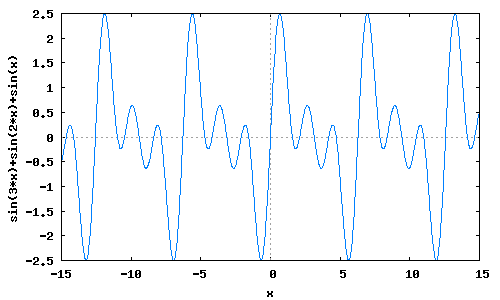
フリーの数式処理ソフトMaximaでピタゴラス音階のグラフを描いてみた.
このような簡単な装置を作って遊んでみると理解が深まるだろう.
フリーの数式処理ソフトMaximaでピタゴラス音階のグラフを描いてみた.
つまり基本波と2倍,3倍の波を足し合わせる
wxplot2d([sin(x)+sin(2*x)+sin(3*x)],
[x,-15,15])$

このようにピタゴラス音律は 1:2:3
で音階を作っていくが, (3^m)/(2^n)=1 となるような自然数 m,n は存在しない.
ただ(3^12)/(2^19)が約 1.013643264770507813 なのでこれを利用して音階を作っている.
このズレがピタゴラス音律の限界で他の音律が登場する理由だ
ただ(3^12)/(2^19)が約 1.013643264770507813 なのでこれを利用して音階を作っている.
このズレがピタゴラス音律の限界で他の音律が登場する理由だ
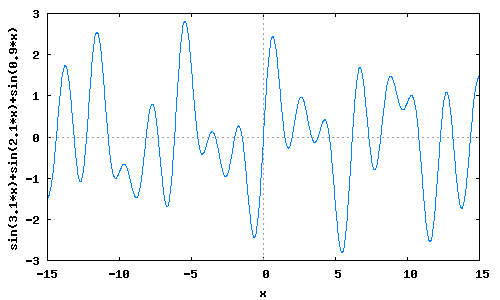
それぞれの波が 1倍,2倍, 3倍より少しズレると
wxplot2d([sin(0.9*x)+sin(2.1*x)+sin(3.1*x)], [x,-15,15])$
打楽器には打楽器の理論がある.このつべ映像見て考えとくれ
wxplot2d([sin(0.9*x)+sin(2.1*x)+sin(3.1*x)], [x,-15,15])$

完全な周期関数ではなくなっている.実際の音はどうちがうか実験して
みると面白い.
(3^12)/(2^19)=1.0136432647705078125 ピタゴラス音律はこれを 1 とするから誤差が出る.ちなみに 3^12 の 12 が 1 オクターブ 12 鍵盤の理由だ.
比が 1 に近くなる組み合わせは他にもあり (3^53)/(2^84)=1.0020903140410861725914298316173
これなら最初のより精度が高い.しかし鍵盤が 53 も必要になるので実用的でないとされたがパソコンを使えば出来る.
(上の計算もパソコンの関数電卓で行った)
53 鍵盤楽器も具体的に周波数を計算して発振器を鳴らせば良い. プログラムが上手な人はプログラムを書けば半ば自動的に演奏できるが,周波数を電卓で計算し手動で発振器をその周波数で鳴らしても良いだろう.
いずれにせよ今までは不可能だと思われていた事がパソコンで出来るようになった.
新しいオーディオの楽しみ方だ.
ドラマーのカレンさんもこんな素晴しい弦の実験ページに貼り付けられてお喜びだろう. 53 鍵盤楽器の考察
(3^12)/(2^19)=1.0136432647705078125 ピタゴラス音律はこれを 1 とするから誤差が出る.ちなみに 3^12 の 12 が 1 オクターブ 12 鍵盤の理由だ.
比が 1 に近くなる組み合わせは他にもあり (3^53)/(2^84)=1.0020903140410861725914298316173
これなら最初のより精度が高い.しかし鍵盤が 53 も必要になるので実用的でないとされたがパソコンを使えば出来る.
(上の計算もパソコンの関数電卓で行った)
53 鍵盤楽器も具体的に周波数を計算して発振器を鳴らせば良い. プログラムが上手な人はプログラムを書けば半ば自動的に演奏できるが,周波数を電卓で計算し手動で発振器をその周波数で鳴らしても良いだろう.
いずれにせよ今までは不可能だと思われていた事がパソコンで出来るようになった.
新しいオーディオの楽しみ方だ.
打楽器には打楽器の理論がある.このつべ映像見て考えとくれ