CR回路の過度出力をMaximaのラプラス変換で計算
CR回路にsinを入れると交流理論では出力は振幅,位相共に変化するが,変化の割合は一定だ.
実際は最初の1回目の出力,2回目の出力…は振幅,位相共に微妙に変化しているから正確には交流理論でなく微分方程式を解か
なければならない.
微分方程式を解く方法は色々あるが,今回はMaximaのラプラス変換で解いてみた.
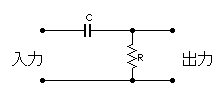
fc=0.159HzのCR回路に0.159Hzの信号を入れた時の出力をフリーの数式処理ソフトMaximaのラプラス
変換で計算してみた.詳しい計算は省略して最後の出力を求める逆ラプラス変換は
ilt((1/(s^2+1)*s/(s+1)),s,x);
結果は
(%o9) sin(x)/2+cos(x)/2-%e^(-x)/2
グラフを描かせると
wxplot2d([(%o9)], [x,0,25])$
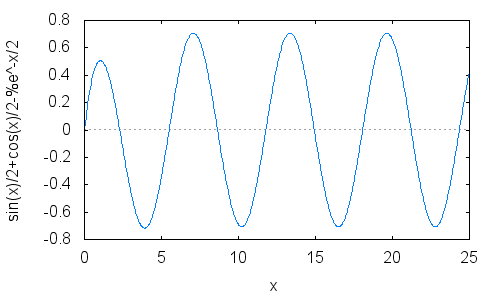
特に最初の振動が小さくなっているのが分かる.(位相も少しズレている)
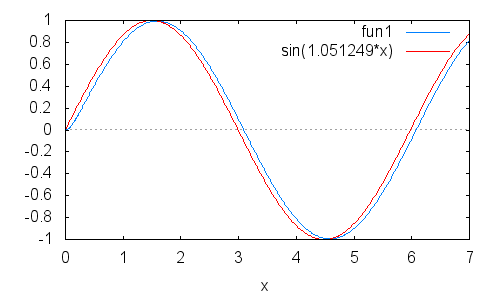
交流理論の出力(赤)と重ねると
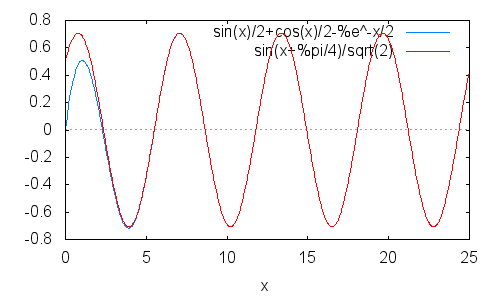
最初の振動の後,ほぼ交流理論通りになっている.
交流理論は無限の過去から無限の未来まで続く振動を扱う事になってるが実際の振動はイキナリ始まる過度現象なので特に最初はズレルのが要点だ.
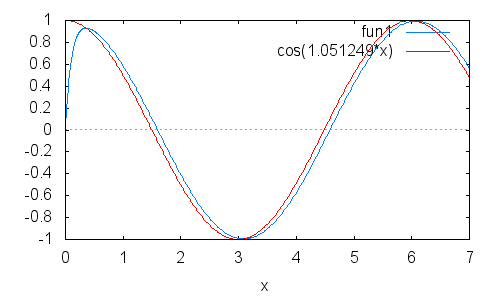
交流理論はSinでもCosでも位相が違うだけで普通他は同じだが,今回CR回路の過度現象を計算していて入力にSinの時と Cosを入れた時では最初の出力が大きく違うので計算間違ったかと思った.
考えてみれば初期条件がSin0=0,Cos0=1と違うので初めの出力が違うのはアタリマエで,過度現象ならではの現象で面白 かった.
最後に入力のsin(緑)と交流理論の出力(赤)と過度現象の 出力(青)を重ねたグラフを
それぞれの波形の振幅だけでなく位相関係にも注意
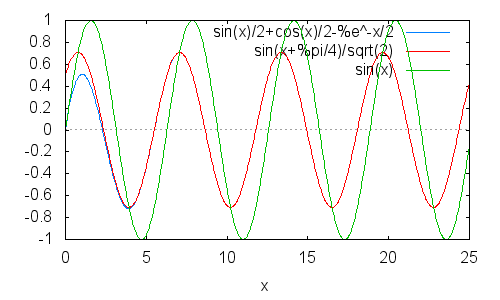
計算を簡単にするために変な周波数で計算しているが,実際の周波数に直すのは難しくない.
それに色々条件を変えて計算したり元の信号も重ねると問題をもっと理解できるだろう.
今回は低域を問題にしたが.CRを逆にすると高域が問題になるのでやってみればさらに良い勉強になる.
フリーの数式処理ソフト
Maxima
やってみたい事
上の計算で分かるようにCR回路は過度現象がありそれを避けるにはさらに低い周波数まで増幅する必要がある.
(これも計算して確かめればよい)
これは位相直線性とも関係する.この辺にこだわって,昭和の頃に直流領域まで増幅するアンプを作ったが,LPを再生するとレコードの反りでウーハーはウハウハ(笑)振動する.それを避けるためローカットフィルターを入れると何の為の位相直線性か?という事になる.
元々LP自体がRIAAで低域や高域を大きく落としたり持ち上げたりで位相直線性もクソもないのでこの実験は止めにした.
しかしPCで音楽を聴くようになってこの問題をもう一度追求してみようかと.
♪よかったね♪
LCR同調回路の過度応答
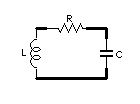
wxmaximaでの実際の計算はコレ(PDF)を参照してもらうとして,ここでは結果だけを説明する.
入力Sinは赤で出 力は青だ.立ち上がりの過度現象は分かりにくいが,同調周波数とズレているので位相がズレているのが分かる.